Tag Archives: RDF

How to Optimize Bridging Blend to Seal the Formation Surface (Part III)

Posted on by

The best way to optimize parameters is to use software like PVI’s BridgePRO, the bridging agent size selection software, to formulate the PSD to most effectively seal the reservoir formation. The software optimization simulation iterates up to 4,600,000 calculations to find the best possible solution according to the target line position, blend volume % of each product, coefficient of determination and the deviation results. The two optimization parameters to determine the best blend formulation are coefficient of determination and deviations.

  1. Coefficient of Determination, R2
    Coefficient of determination [1] is a measure used in statistical model analysis to assess how well a model explains and predicts future outcomes. It is indicative of the level of explained variability in the model. The coefficient, also commonly known as R-square, is used as a guideline to measure the accuracy of the model.
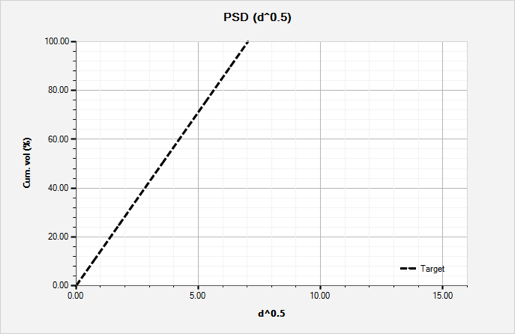
    BridgePRO uses the coefficient of determination to test the goodness of fit of the blend line to the target line. It is expressed as a value between zero and one. A value of one indicates a perfect fit. A value of zero, on the other hand, would indicate that the blend line fails to accurately model the target line.
  2. Deviations
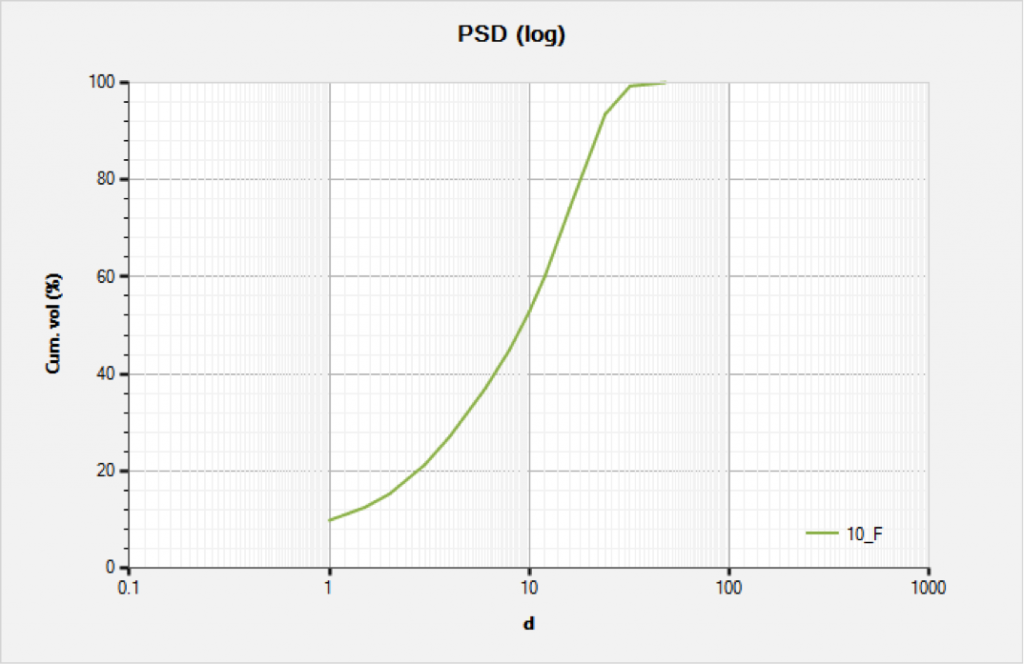
    BridgePRO optimization simulation takes into account the deviation of five points on the formation characteristics target line with the corresponding points on the blend formulation line. The points considered on the cumulative volume % vs. diameter target and blend lines are D10, D25, D50, D75 and D90. Ideally, the best blend line should have the smallest and positive deviations. BridgePRO takes into account both coefficient of determination and the deviations to determine the best blend line slightly on the right side of the target line.

In conclusions, non-damaging RDF design starts with selecting bridging agents with an ideal size distribution to effectively seal the formation surface.

Abrams’ 1/3 rule defines the effectiveness of a bridging material to initial mud solids invasion. However, it does not give optimum size or address the best packing sequence of particle size for minimizing fluid invasion and optimizing sealing.

The ideal packing theory defines the full particle range required to seal all pores, even those created by the bridging agents.

BridgePRO simulation finds the best possible blend formulation according to the target line position, blend volume % of each product, coefficient of determination and the deviation results.

References

  1. Pavel E. Guarisma, Least squares regression, North Carolina State University, http://herkimershideaway.org/apstatistics/ymmsum99/ymm333.htm

How to Optimize Bridging Blend to Seal the Formation Surface (Part I)

Posted on by

Protecting the pay zone from damage is critical to realize the full potential of any well. Reservoir drill-in fluids (RDF) are designed to prevent formation damage due to fluid invasion and solids plugging. A poorly designed RDF may react with the formation fluid creating blockage or restriction for the natural flow of the reservoir. A large range of undesired solid particles from drill solids, fluid chemicals and clay viscosifiers may end up plugging the reservoir pores. The technique for designing a non-damaging RDF is to start with selecting bridging agents with an ideal size distribution to effectively seal the formation surface.

We are going to list a couple of theories behind bridging agent size selection.

  1. Abrams’ rule
    Abrams [1] proposed a rule for formulating minimally invading, non-damaging drill-in fluids. This rule states that the mean particle size of the bridging agent should be equal to or slightly greater than 1/3 the medium pore size of the targeted formation. For example, the rule predicted that those 50μm bridging particles should be effective at sealing pores up to or around 150μm in diameter. Abrams also suggested that the concentration of the bridging solids used should be at least 5% by volume (50 lb/bbl or 150 kg/m3) of the solids in the fluid.
    However, Abrams only addresses the particle size that initiates a bridge. His rule does not give the optimum size or address the best packing sequence of a particle size for minimizing fluid invasion and optimizing sealing. The fluid design using these guidelines tends to use a wide range of particles in an attempt to provide a wide range of bridging capabilities.
  2. Ideal Packing Theory (IPT)
    Ideal Packing Theory can be defined as a full range of particle size distribution required to effectively seal all voids, including those created by bridging agents.
    Fig. 1 shows a typical particle-size distribution for a solid bridging material. Generally, the cumulative volume curve forms an S-shape when plotted on semi-log coordinates. Any commercially available particle-size analysis devices can generate these S-shape plots.

    Fig1. PSD of a Commercial Bridging Product

    Fig 1. PSD of a Commercial Bridging Product

    Kaeuffer [2] employed theories for particles by Furnas and Fuller-Bollomey to generate a simple Ideal Packing Theory also known as the D½ rule. This rule states that ideal packing occurs when the percent of cumulative volume vs. the D½ forms a straight-line relationship as shown in Fig. 2, where D½ is square root of the particle diameter. These subsequent layering of bridging agents results in a tighter and less invading filter cake.

    Fig 2. Ideal Packing

    Fig 2. Ideal Packing

References:

  1. Abrams, A.: “Mud Design to Minimize Rock Impairment Due to Particle Invasion,” JPT (May 1977) 586.
  2. Kaeuffer M.: Determination de L'Optimum deRemplissage Granulometrique et Quelques proprieties S’y Rattachant. Presented at Congres International de I’A.F.T.P.v., Rouen, Oct. 1973